Среднее квадратическое отклонение в Excel

Основная цель работы — научиться вычислять характеристики центра распределения и вариативности.

Среднее арифметическое, мода и медиана

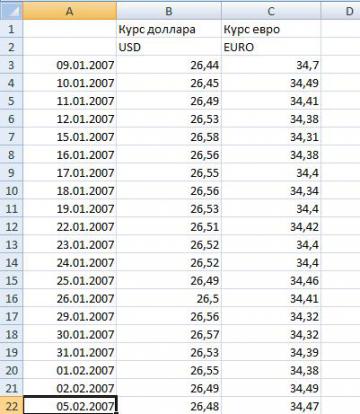
Для вычислений будем использовать 20 наблюдений курсов доллара и евро за 2007 год.

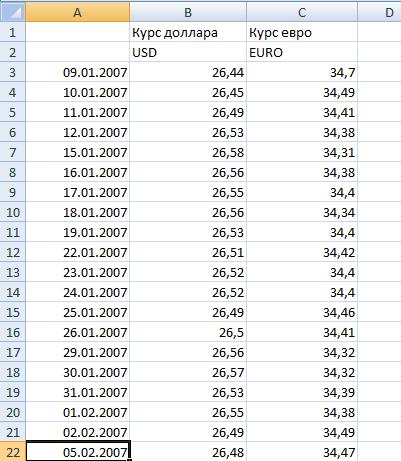
На первом шаге вычисляются среднеарифметические значения курсов валют. Для этого устанавливаем курсор на свободную ячейку столбца В и инициируем команду суммирование. Далее растягиваем формулу вправо. Полученный результат делится на число наблюдений (20). Получаем средние значения для курса доллара и евро. Они выделены на рисунке желтым цветом.

Ниже представлены вычисленные по специальным формулам среднее значение, моду и медиану. Заметим, что среднее значение, вычисленное по заложенной в Excel формулы совпало со значением, рассчитанным первым способом.

Мода — это наиболее часто встречающийся вариант ряда.

Мода вычислена по формуле =МОДА(B3:B22), где B3:B22 — ряд данных.

Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Медиана вычислена по формуле =МЕДИАНА(B3:B22), где B3:B22 — ряд данных.

Дисперсия и среднеквадратичное отклонение

Дисперсия в статистике — это мера разброса данной случайной величины, то есть её отклонения от математического ожидания. Она в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической.

Среднее квардратическое отклонение равно корню из дисперсии.

Вычисления представлены на рисунке ниже.

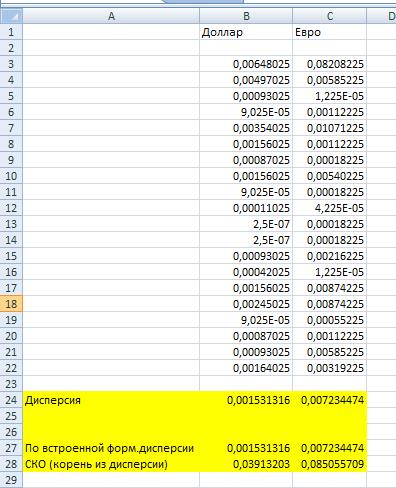
Формула для дисперсии в данном случае =ДИСП(Лист1!B3:B22) Среднее квадратическое отклонение вычислили следующим образом: =КОРЕНЬ(B24), где B24 — ячейка со значением дисперсии.